行测数量关系考试中,抽屉原理类的问题是测查较多的题目类型之一,但是这类题目一般来说并不是很简单,所以更需要我们在复习阶段认真分析题型,摸透其中的解题思路。今天华图教育就带大家一起来分析抽屉问题。
基础知识
例:桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,有的抽屉可以放一个,有的可以放两个,有的可以放五个,但最终我们会发现至少有一个抽屉里面放了至少两个苹果。这一现象就是我们所说的抽屉原理。
抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一个集合里至少有两个元素。
题型特点
①抽屉原理一:将多于n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品件数不少于2。(也可以理解为至少有2件物品在同一个抽屉)
示例:有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子,请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
②抽屉原理二:将多于m×n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品的件数不少于m+1。(也可以理解为至少有m+1件物品在同一个抽屉)
示例:一副扑克牌(去掉两张王牌),每人随意摸两张牌,至少有多少人才能保证他们当中一定有两人所摸两张牌的花色情况是相同的?
例题详解
(一)抽屉原理一
例1
400人中至少有几个人是同月同日出生?
A.1 B.2 C.3 D.4
【解析】B。一年中的366天视为366个抽屉,400个人看作400个物体,由抽屉原理一可以得知:至少有两人是同月同日出生。选择B选项。
例2
从2、4、6、…、30这15个偶数中,任取9个数,证明其中一定有两个数之和是34?
【解析】用题目中的15个偶数制造8个抽屉:凡是抽屉中有两个数的,都具有一个共同的特点:这两个数的和是34。现从题目中的15个偶数中任取9个数,由抽屉原理(因为抽屉只有8个),必有两个数可以在同一个抽屉中(符合上述特点).由制造抽屉的特点,这两个数的和是34。
(二)抽屉原理二
例3
某校派出学生204人上山植树15301株,其中最少一人植树50株,最多一人植树100株,请证明至少有5人植树的株数相同。
【解析】证明:按植树的多少,从50到100株可以构造51个抽屉,则个问题就转化为至少有5人植树的株数在同一个抽屉里。
(用反证法)假设无5人或5人以上植树的株数在同一个抽屉里,那只有5人以下植树的株数在同一个抽屉里,而参加植树的人数为204人,所以,每个抽屉最多有4人,故总株数有: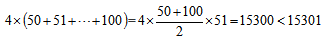 矛盾。因此,至少有5人植树的株数相同。
矛盾。因此,至少有5人植树的株数相同。
对于以上例题练习之后,相信大家对抽屉原理已经掌握得不错了,我们只要把握住问题的两个特点,就能迎刃而解。望广大考生能认真投入,勤加练习,熟能生巧,从而拿下这一类题型。
》》》推荐学习:2024版广西“三支一扶”招募考试专用教材+往年试题
》》》推荐学习:2024年广西三支一扶【综合知识】悦享班
》》》推荐学习:2024年广西三支一扶钻石卷











